Lingkaran merupakan salah satu bentuk geometri yang menjadi pembahasan wajib dalam mata pelajaran matematika. Oleh karena itu, pengetahuan mengenai cara menghitung keliling lingkaran perlu diketahui oleh para siswa yang sedang mempelajari matematika di sekolah.
Alasan lain pentingnya mempelajari lingkaran, selain menjadi materi wajib di sekolah adalah, lingkaran merupakan bentuk yang kerap dijumpai dalam kehidupan sehari-hari. Mulai dari
bentuk roda
yang menjadi komponen penting alat transportasi yang kita gunakan sehari-hari, hingga bentuk makanan favorit banyak orang, seperti pizza atau kue bolu.
Untuk mempelajari materi dasar lingkaran, para siswa bisa mengingat kembali materi tentang unsur-unsur lingkaran, materi rumus luas dan keliling lingkaran, serta rumus luas lingkaran dan keliling lingkaran. Sebagai referensi belajar, berikut ini berbagai materi ajar
tentang lingkaran
Yang akan dipaparkan secara singkat dan jelas dalam artikel ini.
Unsur-Unsur Lingkaran
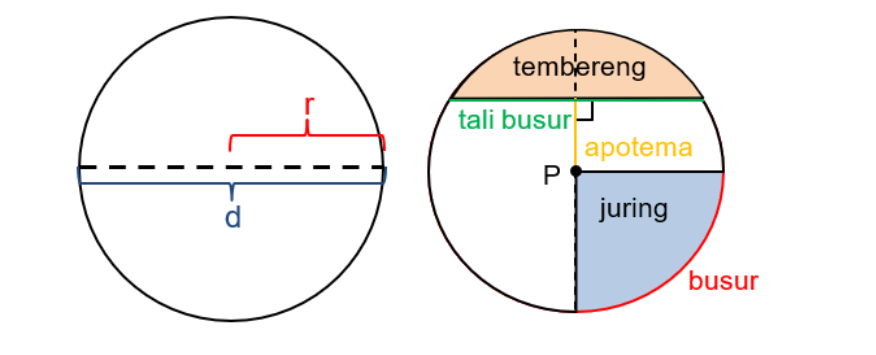
Agar dapat mengerti tentang lingkaran, penting untuk mengetahui definisinya terlebih dulu. Singkatnya, lingkaran merupakan bentuk bidang datar dua dimensi di mana setiap titik pada tepi memiliki jarak yang sama ke sebuah titik tengah tertentu.
Pada saat bersamaan, jarak antara titik tengah dan setiap titik pada keliling lingkaran dikenal sebagai radius atau jari-jari. Selanjutnya, sebuah garis lurus yang membatasi dua titik pada keliling serta melewati pusat dinamakan diameter. Panjang diameter tersebut sama dengan dua kali ukuran jari-jarinya.
Lingkaran merupakan suatu bentuk dua dimensi yang memiliki sejumlah bagian penyusunnya. Bagian-bagian ini dikenal dengan istilah elemen-elemen lingkaran. Elemen-elemen dalam sebuah lingkaran meliputi:
Titik Pusat (P)
Titik yang berada di bagian paling center dari lingkaran dan disebut sebagai titik pusat. Semua titik pada keliling lingkaran merujuk kepada titik pusat ini.
Jari-jari (r)
Garis-garis raya merupakan segmen langsung yang membatasi titik tengah dan setiap posisi di sepanjang keliling lingkaran. Panjang dari salah satu bagian tersebut menunjukkan jarak antara sentral lingkaran hingga tepiannya.
Diameter (d)
Garis lurus yang melintasi pusat lingkaran dan menghubungkan dua titik pada lingkaran. Garis ini panjangnya dua kali jari-jari.
Busur Lingkaran
Bagian dari keliling lingkaran. Komponen ini berbentuk garis melengkung pada tepian lingkaran.
Tali Busur
Garispenghubung antara dua titik pada keliling lingkaran tanpa melewati tengahnya.
Juring Lingkaran
Area di dalam lingkaran yang ditentukan oleh dua radius dan satu busur.
Tembereng
Bagian ini adalah area di dalam lingkaran yang dikelilingi oleh tali busur serta lengannya.
Apotema
Garis terpendek yang menghubungi pusat lingkaran dengan tali busurnya. Elemen ini bersifat tegak lurus terhadap tali busur tersebut.
Lantas, bagaimana cara menghitung luas dan keliling lingkaran?
Bagaimana Cara Menentukan Luas serta Keliling Lingkaran
Agar dapat memahami dengan lengkap tentang bab lingkaran, para pelajar perlu tahu bagaimana mencari luas serta keliling dari sebuah lingkaran. Dalam hal ini, terdapat formula khusus untuk menghitung luas lingkaran yang bisa digunakan oleh siswa agar mereka mampu mendapatkan hasil akurat atas ukuran lingkaran tersebut.
Demikian pula untuk memastikan keliling sebuah lingkaran, terdapat formula khusus untuk perhitungan keliling lingkaran yang dapat membantu dalam mendapatkan hasil akurat.
Untuk mendapat gambaran yang lengkap, berikut ini akan dipaparkan secara ringkas materi luas dan keliling lingkaran, termasuk rumus luas lingkaran, keliling lingkaran, juga contoh soal dan jawabannya.
Cara Menghitung Luas Lingkaran dan Contoh Soal
Luas lingkaran adalah jumlah area yang dibatasi oleh keliling lingkaran. Luas lingkaran dapat dihitung dengan menggunakan jari-jari lingkaran. Jika yang diketahui diameternya, maka kita harus mengubah diameter menjadi jari-jari lingkaran.
Untuk mengubah diameter menjadi jari-jari, kita harus membagi diameter dengan 2.
Berikut ini rumus luas lingkaran:
Rumus Luas Lingkaran (L)
L = πr²
Di mana:
- L = Luas lingkaran
- π (pi) = 3,14 atau 22/7
- r = jari-jari lingkaran
Contoh soal:
1. Sebuah lapangan berbentuk lingkaran memiliki diameter 14 meter. Berapakah luas lapangan tersebut!
Jawab:
Diketahui diameter lapangan = 14 m, maka jari-jari (r) = 14/2 = 7 m
Luas Lingkaran (L) = π x r²
L = 22/7 × 49 m²
L = 22 × 7 m²
L = 154 m²
Jadi, luas lapangan tersebut adalah 154 m².
2. Tentukan luas lingkaran yang memiliki jari-jari 21 cm!
Jawab:
Diketahui lingkaran dengan r=21 cm
Luas lingkaran (L) = π dikali dengan jari-jari kuadrat
L = 22/7 × 21 × 21
L = 22/7 × 441
L = 22 oleh 63
L = 1.386 cm²
Jadi, luas lingkaran tersebut adalah 1.386 cm².
3. Alas lantai yang berbentuk lingkaran memiliki jari-jari sepanjang 7 cm. Kiranya Anda dapat menghitung luas dari dasar lantai itu dengan menggunakan nilai π sama dengan 22/7!
Jawab:
Diberikan: jari-jari = 7 cm
L = π × r²
L = 22/7 x 7 x 7
L = 22 x 7
L = 154 cm²
Jadi, luas lingkaran adalah 154 cm².
Langkah untuk Menentukan Keliling Lingkaran serta Teladan Permasalahan
Keliling lingkaran adalah busur terpanjang pada suatu lingkaran, atau panjang lintasan yang membentuk lingkaran tersebut.
Ada dua cara untuk menghitung keliling lingkaran, yaitu bisa dihitung jika diketahui jari-jari (r) atau bisa dihitung jika diketahui diameter (d).
Berikut ini rumus keliling lingkaran:
Rumus Keliling Lingkaran (K)
K = 2πr (apabila panjang jari-jarinya telah diberikan)
K = πd (apabila diameter lingkaran telah diberikan)
Di mana:
- K = Keliling lingkaran
- π (pi) = 3,14 atau 22/7
- r = jari-jari lingkaran
- d = diameter lingkaran
Angka π (pi) dalam formula lingkaran tersebut bergantung kepada permasalahan yang diberikan. Apabila jejari atau diameter bulat adalah kelipatan dari tujuh, umumnya dipakai angka 22/7. Sedangkan, untuk persoalan bulat lainnya, akan diaplikasikan nilai 3,14.
Contoh soal:
1. Sebuah roda gerobak memiliki jari-jari 35 cm. Berapakah keliling roda gerobak tersebut?
Jawab:
Diketahui jari-jari (r) = 35 cm
Keliling Lingkaran (K) = 2πr
K = 2 × 22/7 × 35 cm
K = 220 cm
Maka, lingkar roda gerobak itu sebesar 220 sentimeter.
2. Hitunglah keliling dasar bangku yang berbentuk lingkaran dengan jari-jari sebesar 10 cm?
Jawab:
Diketahui jari-jari sebesar 10 cm.
Keliling Lingkaran (K) = 2 kali π dikali jari-jari
K = 2 x 3,14 x 10 cm
K = 62,8 cm
Maka, diameter kursi yang berbentuk lingkaran itu adalah 62,8 cm.
3. Roda dengan jari-jari sebesar 14 cm itu berapa kelilingnya?
Jawab:
Diketahui radius (r) = 14 cm
Keliling Lingkaran (K) = 2 × π × r
K = 2 × 22/7 × 14 cm
K = 2 × 22 × 2
K = 88 cm
Oleh karena itu, keliling dari roda tersebut adalah 88 cm.

Berikut ini adalah penjelasan ringkas tentang komponen-komponen dari sebuah lingkaran, termasuk area dan perimeter lingkaran beserta formula-formulanya. Di samping itu, telah dibahas pula beberapa hal terkait tersebut.
contoh soal
yang bisa dipelajari.
Melalui pengkajian mendalam terhadap bermacam-macam persoalan serta konten mengenai bangun datar lingkaran dengan usaha sendiri, para pelajar yang tengah menekuni topik lingkaran tersebut dapat mencapai pemahaman yang lebih baik dan kelancaran dalam penyelesaian tugasnya.
berbagai soal
tentang lingkaran saat menghadapi ujian di sekolah.

